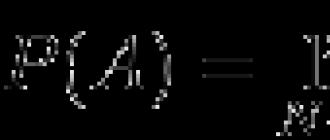Определения вероятности

Классическое определение

Классическое "определение" вероятности исходит из понятия равновозможности как объективного свойства изучаемых явлений. Равновозможность является неопределяемым понятием и устанавливается из общих соображений симметрии изучаемых явлений. Например, при подбрасывании монетки исходят из того, что в силу предполагаемой симметрии монетки, однородности материала и случайности (непредвзятости) подбрасывания нет никаких оснований для предпочтения "решки" перед "орлом" или наоборот, то есть выпадение этих сторон можно считать равновозможными (равновероятными).

Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идет об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел.

Классическое определение вероятности можно сформулировать следующим образом:

Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:

Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно очевидно 36 (6 возможностей на каждой кости). Оценим вероятность выпадения 7 очков. Получение 7 очков возможно следующими способами: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих событию A - получению 7 очков. Следовательно, вероятность будет равна 6/36=1/6. Для сравнения вероятность получения 12 очков или 2 очков равна всего 1/36 - в 6 раз меньше.

Геометрическое определение

Несмотря на то, что классическое определение является интуитивно понятным и выведенным из практики, оно, как минимум не может быть непосредственно применено в случае, если количество равновозможных исходов бесконечно. Ярким примером бесконечного числа возможных исходов является ограниченная геометрическая область G, например, на плоскости, с площадью S. Случайно "подброшенная" "точка" с равной вероятностью может оказаться в любой точке этой области. Задача заключается в определении вероятности попадания точки в некоторую подобласть g с площадью s. В таком случая обобщая классическое определение можно прийти к геометрическому определению вероятности попадания в подобласть :

В виду равновозможности вероятность эта не зависит от формы области g, она зависит только от ее площади. Данное определение естественно можно обобщить и на пространство любой размерности, где вместо площади использовать понятие "объема". Более того, именно такое определение приводит к современному аксиоматическому определению вероятности. Понятие объема обобщается до понятия "меры" некоторого абстрактного множества, к которой предъявляются требования, которыми обладает и "объем" в геометрической интерпретации - в первую очередь, это неотрицательность и аддитивность.

Частотное (статистическое) определение

Классическое определение при рассмотрении сложных проблем наталкивается на трудности непреодолимого характера. В частности, в некоторых случаях выявить равновозможные случаи может быть невозможно. Даже в случае с монеткой, как известно существует явно не равновероятная возможность выпадения "ребра", которую из теоретических соображений оценить невозможно (можно только сказать, что оно маловероятно и то это соображение скорее практическое). Поэтому еще на заре становления теории вероятностей было предложено альтернативное "частотное" определение вероятности. А именно, формально вероятность можно определить как предел частоты наблюдений события A, предполагая однородность наблюдений (то есть одинаковость всех условий наблюдения) и их независимость друг от друга:

где - количество наблюдений, а - количество наступлений события .

Несмотря на то, что данное определение скорее указывает на способ оценки неизвестной вероятности - путем большого количества однородных и независимых наблюдений - тем не менее в таком определении отражено содержание понятия вероятности. А именно, если событию приписывается некоторая вероятность, как объективная мера его возможности, то это означает, что при фиксированных условиях и многократном повторении мы должны получить частоту его появления, близкую к (тем более близкую, чем больше наблюдений). Собственно, в этом заключается исходный смысл понятия вероятности. В основе лежит объективистский взгляд на явления природы. Ниже будут рассмотрены так называемые законы больших чисел, которые дают теоретическую основу (в рамках излагаемого ниже современного аксиоматического подхода) в том числе для частотной оценки вероятности.

Аксиоматическое определение

В современном математическом подходе вероятность задаётся аксиоматикой Колмогорова . Предполагается, что задано некоторое пространство элементарных событий . Подмножества этого пространства интерпретируются как случайные события . Объединение (сумма) некоторых подмножеств (событий) интерпретируется как событие, заключающееся в наступлении хотя бы одного из этих событий. Пересечение (произведение) подмножеств (событий) интерпретируется как событие, заключающееся в наступлении всех этих событий. Непересекающиеся множества интерпретируются как несовместные события (их совместное наступление невозможно). Соответственно, пустое множество означает невозможное событие.

Вероятностью (вероятностной мерой ) называется мера (числовая функция) , заданная на множестве событий, обладющая следующими свойствами:

В случае если пространство элементарных событий X конечно , то достаточно указанного условия аддитивности для произвольных двух несовместных событий, из которого будет следовать аддитивность для любого конечного количества несовместных событий. Однако, в случае бесконечного (счетного или несчетного) пространства элементарных событий этого условия оказывается недостаточно. Требуется так называемая счетная или сигма- аддитивность , то есть выполнение свойства аддитивности для любого не более чем счетного семейства попарно несовместных событий. Это необходимо для обеспечения "непрерывности" вероятностной меры.

Вероятностная мера может быть определена не для всех подмножеств множества . Предполагается, что она определена на некоторой сигма-алгебре подмножеств . Эти подмножества называются измеримыми по данной вероятностной мере и именно они являются случайными событиями. Совокупность - то есть множество элементарных событий, сигма-алгебра его подмножеств и вероятностная мера - называется вероятностным пространством .

Непрерывные случайные величины. Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х) . Однако их можно задать с помощью функции распределения вероятностей F(х) . Эта функция определяется точно так же, как и в случае дискретной случайной величины:

Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х . Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины. Случайная величина называется непрерывной , если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству

Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств равна площади криволинейной трапеции с основанием , ограниченной сверху кривой (рис. 6).

Так как , а на основании формулы (22)

Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х , где функция непрерывна. Это следует из того, что F(х) в этих точках дифференцируема. На основании формулы (23), полагая x 1 =x , , имеем

В силу непрерывности функции F(х) получим, что

Следовательно

Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю . Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств

Имеют одинаковую вероятность, т.е.

В самом деле, например,

так как Замечание. Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение x 1 как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение x 1 . Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение. Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска. Пример. Плотность распределения непрерывной случайной величины задана следующим образом:

График функции представлен па рис. 7. Определить вероятность того, что случайная величина примет значение, удовлетворяющее неравенствам .Найти функцию распределения заданной случайной величины. (Решение )

Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин - равномерному и нормальному распределениям.

* Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода. ** Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,

Так как интеграл

есть величина постоянная.

Зависимые и независимые события. Условная вероятность

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Пример 3. Монета брошена два раза. Вероятность появления "герба" в первом испытании (событие ) не зависит от появления или не появления "герба" во втором испытании (событие ). В свою очередь, вероятность появления "герба" во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.

Несколько событий называются независимыми в совокупности , если любое из них не зависит от любого другого события и от любой комбинации остальных.

События называются зависимыми , если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события , называется условной вероятностью события и обозначается .

Условие независимости события от события записывают в виде , а условие его зависимости - в виде . Рассмотрим пример вычисления условной вероятности события.

Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.

Решение. Обозначим извлечение изношенного резца в первом случае, а - извлечение нового. Тогда . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.

Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:

Следовательно, вероятность события зависит от того, произошло или нет событие .

Пло́тность вероя́тности - один из способов задания вероятностной меры на евклидовом пространстве . В случае, когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины .

Плотность вероятности Пусть является вероятностной мерой на, то есть определено вероятностное пространство, где обозначает борелевскую σ-алгебру на. Пусть обозначает меру Лебега на.

Определение 1. Вероятность называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция такая, что

,

где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть - произвольное измеримое пространство, а и - две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру через меру в виде

то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают

События А, В называются независимыми , если вероятности каждого из них не зависит от того, произошло или нет другое событие. Вероятности независимых событий называются безусловными .

События А, В называются зависимыми , если вероятность каждого из них зависит от того, произошло или нет другое событие. Вероятность события В, вычисленная в предположении, что другое событие А уже осуществилось, называется условной вероятностью .

Если два события А и В – независимые, то справедливы равенства:

Р(В) = Р(В/А), Р(А) = Р(А/В) или Р(В/А) – Р(В) = 0 (9)

Вероятность произведения двух зависимых событий А, В равна произведению вероятности одного из них на условную вероятность другого:

Р(АВ) = Р(В) ∙ Р(А/В) или Р(АВ) = Р(А) ∙ Р(В/А) (10)

Вероятность события В при условии появления события А:

Вероятность произведения двух независимых событий А, В равна произведению их вероятностей:

Р(АВ) = Р(А) ∙ Р(В) (12)

Если несколько событий попарно независимы, то отсюда еще не следует их независимость в совокупности.

События А 1 , А 2 , …, А n (n>2) называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.

Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Р(А 1 ∙А 2 ∙А 3 ∙…∙А n) = Р(А 1)∙Р(А 2)∙Р(А 3)∙…∙Р(А n). (13)

Конец работы -

Эта тема принадлежит разделу:

Конспект лекций основные понятия теории вероятностей и статистики, используемые в эконометрике

Казанский государственный.. финансово экономический институт.. кафедра статистики и эконометрики..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Дискретная случайная величина
Наиболее полным, исчерпывающим описанием дискретной СВявляется ее закон распределения.Законом распределения случайной величины называется всякое соотношение, устан

Непрерывная случайная величина
Для непрерывной СВ нельзя определить вероятность того, что она примет некоторое конкретное значение (точечную вероятность). Так как в любом интервале содержится бесконечное число значений, то вероя

Взаимосвязь случайных величин
Многие экономические показатели определяются несколькими числами, являясь многомерными СВ. Упорядоченный набор Х=(Х1, Х2, …, Хn) случайных в

Выборочное наблюдение
Генеральной совокупностьюназывается множество всех возможных значений или реализаций исследуемой СВ Х при данном реальном комплексе условий. Выборкой

Вычисление выборочных характеристик
Для любой СВ Х кроме определения ее функции распределения желательно указать числовые характеристики, важнейшими из которых является: - математическое ожидание; - дисперсия

Нормальное распределение
Нормальное распределение (распределение Гаусса) является предельным случаем почти всех реальных распределений вероятности. Поэтому оно используется в очень большом числе реальных приложений теории

Распределение Стьюдента
Пусть СВ U ~ N (0,1), СВ V – независимая от U величина, распределенная по закону χ2 с n степенями свободы. Тогда величина

Распределение Фишера
Пусть V и W – независимые СВ, распределенные по закону χ2 со степенями свободы v1 = m и v2 = n соответственно. Тогда величина

Точечные оценки и их свойства
Пусть оценивается некоторый параметр наблюдаемой СВ

Состоятельность
Оценка называется несмещенной оценкой параметра, если ее математи

Свойства выборочных оценок
На начальном этапе в качестве оценки той или иной числовой характеристики (математического ожидания, дисперсии и т.п.) берется выборочная числовая характеристика. Затем, исследуя эту оценку, ее уто

Доверительный интервал для дисперсии нормальной СВ
Пусть Х ~ N (m, σ2) причем и - неизвестны. Пусть для оценки

Критерии проверки. Критическая область
Проверку статистической гипотезы осуществляют на основании данных выборки.Для этого используют специально подобранную СВ (статистику, критерий), точное или приближенное значение которой известно. Э

Определение 1. Событие А называется зависимым от события В, если вероятность появления события А зависит от того, произошло или не произошло событие В. Вероятность того, что произошло событие А при условии, что произошло событие В, будем обозначать и называть условной вероятностью события А при условии В.

Пример 1. В урне находится 3 белых шара и 2 черных. Из урны вынимается один шар (первое вынимание), а затем второй (второе вынимание). Событие В - появление белого шара при первом вынимании. Событие А - появление белого шара при втором вынимании.

Очевидно, что вероятность события А, если событие В произошло, будет

Вероятность события Л при условии, что событие В не произошло (при первом вынимании появился черный шар), будет

Видим, что

Теорема 1. Вероятность совмещения двух событий равняется произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т. е.

Доказательство. Доказательство приведем для событий, которые сводятся к схеме урн (т. е. в случае, когда применимо классическое определение вероятности).

Пусть в урне шаров, при этом белых, черных. Пусть среди белых шаров шаров с отметкой «звездочка», остальные чисто белые (рис. 408).

Из урны вынимается один шар. Какова вероятность события вынуть белый шар с отметкой «звездочка»?

Пусть В - событие, состоящее в появлении (белого шара, А - событие, состоящее в появлении шара с отметкой «звездочка». Очевидно,

Вероятность появления белого шара со «звездочкой при условии, что появился белый шар, будет

Вероятность появления белого шара со «звездочкой» есть Р (А и В). Очевидно,

Подставляя в (5) левые части выражений (2), (3) и (4), получаем

Равенство (1) доказано.

Если рассматриваемые события не укладываются в классическую - схему, то формула (1) служит для определения условной вероятности. А именно, условная вероятность события А при условии осуществления события В опрёделяется с помощью

Замечание 1. Применим последнюю формулу к выражению :

В равенствах (1) и (6) левые части равны, так как это одна и та же вероятность, следовательно, равны и правые. Поэтому можем написать равенство

Пример 2. Для случая примера 1, приведенного в начале этого параграфа, имеем По формуле (1) получаем Вероятность Р(А и В) легко вычисляется и непосредственно.

Пример 3. Вероятность изготовления годного изделия данным станком равна 0,9. Вероятность появления изделия 1-го сорта среди годных изделии есть 0,8. Определить вероятность изготовления изделия 1-го сорта данным станком.

Решение. Событие В - изготовление годного изделия данным станком, событие А - появление изделия 1-го сорта. Здесь Подставляя в формулу (1), получаем искомую вероятность

Теорема 2. Если событие А может осуществиться только при выполнении одного из событий которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

Формулд (8) называется формулой полной вероятности. Доказательство. Событие А может произойти при выполнении любого из совмещенных событий

Следовательно, по теореме о сложение вероятностей получаем

Заменяя слагаемые правой части по формуле (1), получим равенство (8).

Пример 4. По цели произведено три последовательных выстрела. Вероятность попадания при первом выстреле при втором при третьем При одном попадании вероятность поражения цели при двух попаданиях , при трех попаданиях Определить вероятность пфаженйя цели при трех выстрелах (событие А).

Решение. Рассмотрим полную группу несовместных событий:

Было одно попадание;

Р(А)= 1 - 0,3 = 0,7.

3. Теорема сложения вероятностей противоположных событий

Противоположными называют два несовместных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать . Противоположное событие состоит в непоявлении событияА.

Теорема. Сумма вероятностей противоположных событий равна единице:

Р(А)+Р()= 1.

Пример 4. В ящике имеется 11 деталей, из которых 8 стандартных. Найти вероятность того, что среди 3 наудачу извлеченных деталей есть хотя бы одна бракованная.

Решение. Задачу можно решить двумя способами.

1 способ . События “среди извлеченных деталей есть хотя бы одна бракованная” и “среди извлеченных деталей нет ни одной бракованной” - противоположные. Обозначим первое событие через А, а второе через :

Р(А) =1 - Р() .

Найдем Р(). Общее число способов, которыми можно извлечь 3 детали из 11 деталей, равно числу сочетаний
. Число стандартных деталей равно 8; из этого числа деталей можно
способами извлечь 3 стандартных детали. Поэтому вероятность того, что среди извлеченных 3 деталей нет ни одной нестандартной, равна:

По теореме сложения вероятностей противоположных событий искомая вероятность равна: P(A)=1 - P()=

2 способ. Событие А - "среди извлеченных деталей есть хотя бы одна бракованная" - может реализоваться, как появление:

или события В - "извлечены 1 бракованная и 2 не бракованные детали",

или события С - "извлечены 2 бракованные и 1 не бракованная детали",

или события D - "извлечены 3 бракованные детали".

Тогда A = B + C + D . Так как события B , C и D несовместные, то можно применить теорему сложения вероятностей несовместных событий:

4. Теорема умножения вероятностей независимых событий

Произведением двух событий А и В называют событие C =АВ, состоящее в совместном появлении (совмещении) этих событий.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, событие АВС состоит в совмещении событий А, В и С .

Два события называют независимыми , если вероятность одного из них не зависит от появления или непоявления другого.

Теорема. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Р(АВ)=Р(А)  Р(В).

Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Р(А 1 А 2 ... А n ) = Р(А 1 ) · Р(А 2 )...Р(А n ).

Пример 5. Найти вероятность совместного появления герба при одном бросании двух монет.

Решение . Обозначим события: А - появление герба на первой монете, В - появление герба на второй монете, С - появление герба на двух монетах С=АВ .

Вероятность появления герба первой монеты:

Р(А) =.

Вероятность появления герба второй монеты:

Р(В) =.

Так как события А и В независимые, то искомая вероятность по теореме умножения равна:

Р(С)=Р(АВ) = Р(А)  Р(В) = =.

Пример 6. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Решение . Вероятность того, что из первого ящика вынута стандартная деталь (событие А):

Р(А) =

Вероятность того, что из второго ящика вынута стандартная деталь (событие В):

Вероятность того, что из третьего ящика вынута стандартная деталь (событие С ):

Р(С)=

Так как события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения) paвна:

P(ABC)=P(A)  P(B)  P(C)= 0,8 0,70,9 = 0,504.

Пример 7. Вероятности появления каждого из двух независимых событий А 1 и А 2 соответственно равны р 1 и р 2. Найти вероятность появления только одного из этих событий.

Решение . Введем обозначения событий:

В 1 – появилось только событие А 1 ; В 2 – появилось только событие А 2 .

Появление события В 1 равносильно появлению события А 1 2 (появилось первое событие и не появилось второе), т.е. В 1 = А 1 2 .

Появление события В 2 равносильно появлению события 1 А 2 (не появилось первое событие и появилось второе), т.е. В 1 = 1 А 2 .

Таким образом, чтобы найти вероятность появления только одного из событий А 1 или А 2 , достаточно найти вероятность появления одного, безразлично какого из событий В 1 и В 2 . События В 1 и В 2 несовместны, поэтому применима теорема сложения несовместных событий:

Р(В 1 +В 2 ) = Р(В 1 ) + Р(В 2 ) .

Независимые события

При практическом применении вероятностно-статистических методов принятия решений постоянно используется понятие независимости. Например, при применении статистических методов управления качеством продукции говорят о независимых измерениях значений контролируемых параметров у включенных в выборку единиц продукции, о независимости появления дефектов одного вида от появления дефектов другого вида, и т.д. Независимость случайных событий понимается в вероятностных моделях в следующем смысле.

Определение 2. События А и В называются независимыми, если Р(АВ) = Р(А) Р(В). Несколько событий А , В , С ,… называются независимыми, если вероятность их совместного осуществления равна произведению вероятностей осуществления каждого из них в отдельности: Р (АВС …) = Р (А )Р (В )Р (С )…

Это определение соответствует интуитивному представлению о независимости: осуществление или неосуществление одного события не должно влиять на осуществление или неосуществление другого. Иногда соотношение Р (АВ ) = Р (А ) Р (В |A ) = P (B )P (A |B ), справедливое при P (A )P (B) > 0, называют также теоремой умножения вероятностей.

Утверждение 1. Пусть события А и В независимы. Тогда события и независимы, события и В независимы, события А и независимы (здесь - событие, противоположное А , и - событие, противоположное В ).

Действительно, из свойства в) в (3) следует, что для событий С и D , произведение которых пусто, P (C + D ) = P (C ) + P (D ). Поскольку пересечение АВ и В пусто, а объединение есть В , то Р(АВ) + Р(В) = Р(В). Так как А и В независимы, то Р(В) = Р(В) - Р(АВ) = Р(В) - Р(А)Р(В) = Р(В)(1 - Р(А)). Заметим теперь, что из соотношений (1) и (2) следует, что Р() = 1 – Р(А). Значит, Р(В) = Р()Р(В).

Вывод равенства Р(А) = Р(А)Р() отличается от предыдущего лишь заменой всюду А на В , а В на А .

Для доказательства независимости и воспользуемся тем, что события АВ, В, А, не имеют попарно общих элементов, а в сумме составляют все пространство элементарных событий. Следовательно, Р (АВ) + Р(В) + Р(А) + Р() = 1. Воспользовавшись ранее доказанными соотношениями, получаем, что Р(В)= 1 - Р (АВ) - Р(В)(1 - Р(А)) - Р(А)(1 - Р(В))= (1 – Р(А))(1 – Р(В)) = Р()Р(), что и требовалось доказать.

Пример 3. Рассмотрим опыт, состоящий в бросании игрального кубика, на гранях которого написаны числа 1, 2, 3, 4, 5,6. Считаем, что все грани имеют одинаковые шансы оказаться наверху. Построим соответствующее вероятностное пространство. Покажем, что события «наверху – грань с четным номером» и «наверху – грань с числом, делящимся на 3» являются независимыми.

Разбор примера. Пространство элементарных исходов состоит из 6 элементов: «наверху – грань с 1», «наверху – грань с 2»,…, «наверху – грань с 6». Событие «наверху – грань с четным номером» состоит из трех элементарных событий – когда наверху оказывается 2, 4 или 6. Событие «наверху – грань с числом, делящимся на 3» состоит из двух элементарных событий – когда наверху оказывается 3 или 6. Поскольку все грани имеют одинаковые шансы оказаться наверху, то все элементарные события должны иметь одинаковую вероятность. Поскольку всего имеется 6 элементарных событий, то каждое из них имеет вероятность 1/6. По определению 1событие «наверху – грань с четным номером» имеет вероятность ½, а событие «наверху – грань с числом, делящимся на 3» - вероятность 1/3. Произведение этих событий состоит из одного элементарного события «наверху – грань с 6», а потому имеет вероятность 1/6. Поскольку 1/6 = ½ х 1/3, то рассматриваемые события являются независимыми в соответствии с определением независимости.